Baumfraktale: Forscher erklären, wie eine universelle mathematische Regel das Baumgeäst bestimmt
Forscher haben herausgefunden, dass sich die Verzweigung von Ästen mathematisch mit fraktalen Gesetzmäßigkeiten beschreiben lässt. In künstlerischen Darstellungen hängt es sogar von diesen Regelmäßigkeiten ab, ob wir einen Baum als solchen erkennen oder nicht.

Die Verzweigung von Bäumen folgt einer universellen mathematischen Gesetzmäßigkeit. Dies gilt nicht nur für reale Bäume, sondern auch für deren Darstellungen in der Kunst. Zwei Forschende haben herausgefunden, dass dieses Muster entscheidend dafür ist, ob ein gemalter Baum als solcher erkannt wird. Wird diese Regel gebrochen, verschwimmt die Darstellung in subjektiven Interpretationen.
Auch Bäume weisen eine fast fraktale Struktur auf: Ihre Äste teilen sich vom Stamm bis zu den feinsten Verzweigungen in einem stets gleichbleibenden Muster. Diese Form begünstigt Stabilität und eine effiziente Nährstoffversorgung.
Was ist der Radius-Skalierungsexponent α?
Jingyi Gao von der University of Wisconsin und Mitchell Newberry von der University of New Mexico haben dieses Muster nun wissenschaftlich untersucht. Sie analysierten nicht nur reale Bäume, sondern auch künstlerische Darstellungen aus verschiedenen Epochen und Stilen. Dabei konzentrierten sie sich darauf, wie die Dicke der Äste mit der Anzahl der Verzweigungen zusammenhängt. Das Ergebnis: Eine mathematische Formel beschreibt dieses Muster und bestätigt eine Regel, die bereits Leonardo da Vinci erkannt hatte.
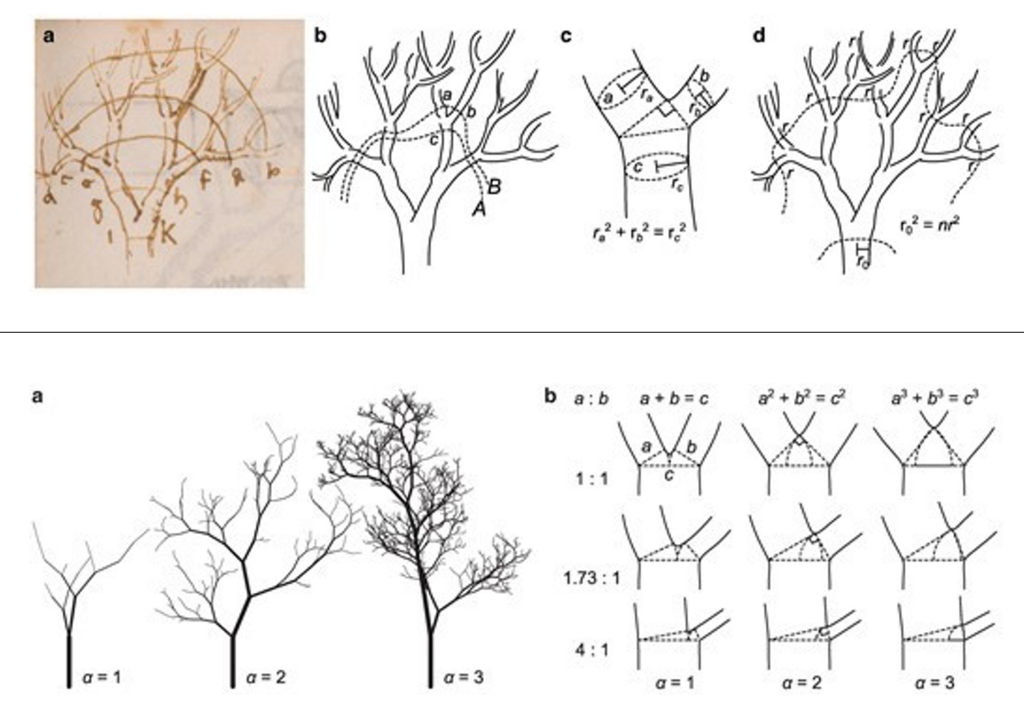
Da Vinci stellte fest, dass die Summe der Durchmesser aller Zweige an einer Gabelung in etwa der Dicke des ursprünglichen Astes entspricht. Die Forschenden drückten dies mathematisch aus: Der sogenannte Radius-Skalierungsexponent α gibt an, wie sich die Astdurchmesser verändern. Bei einer klassischen Gabelung in zwei Äste beträgt dieser Wert 2, wie es schon da Vinci beschrieb.
„Grauer Baum“ und „Blühender Apfelbaum“
Gao und Newberry fanden heraus, dass in künstlerischen Darstellungen von Bäumen der Wert für α zwischen 1,5 und 2,8 liegt – genau der Bereich, der auch bei echten Bäumen vorkommt. „Wir haben hier etwas Universelles entdeckt, das für alle Bäume gilt, egal ob in der Natur oder in der Kunst“, sagt Newberry. Die natürliche Skalierung sorgt dafür, dass ein Betrachter das Motiv sofort als Baum erkennt.
Selbst in abstrakter Kunst bleibt dieses Prinzip erhalten. Ein Beispiel ist Piet Mondrians kubistisches Gemälde „Grauer Baum“. Obwohl dort keine realistischen Verzweigungen oder Farben zu sehen sind, entspricht die Verteilung der Astdurchmesser der natürlichen Skalierung. Dies trägt dazu bei, dass das Motiv als Baum wahrgenommen wird.
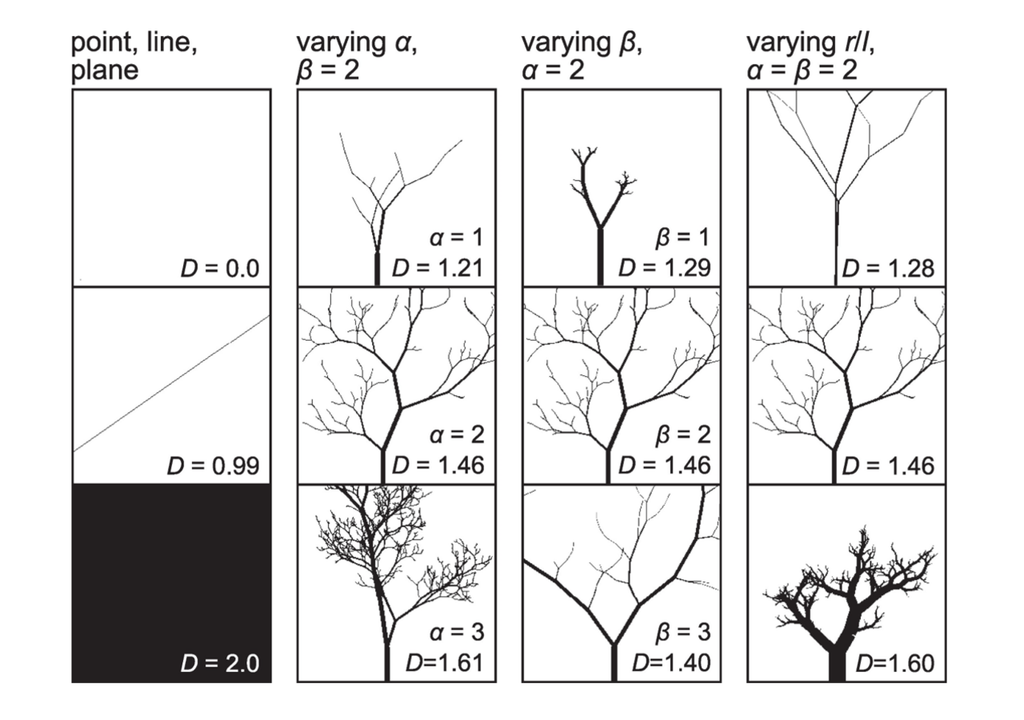
Anders verhält es sich bei Mondrians späterem Werk „Blühender Apfelbaum“. Hier liegt der α-Wert bei 5,7 und weicht damit stark von natürlichen Werten ab. Der Baum sei in gewisser Weise „verschwunden“, so Newberry. Stattdessen sehen Betrachter verschiedene andere Formen, wie Wasser, Boote, Fischschuppen oder Tanzfiguren.
Die Erkenntnisse zeigen, dass mathematische Prinzipien sowohl in der Natur als auch in der Kunst eine fundamentale Rolle spielen. Die Forschenden schlagen vor, den Skalierungsparameter α gezielt in der ästhetischen Forschung sowie in den Naturwissenschaften einzusetzen. Ihre Studie verdeutlicht, wie eng Kunst und Wissenschaft miteinander verbunden sind.
Quellenhinweis
Gao, J., & Newberry, M. G. (2025): Scaling in branch thickness and the fractal aesthetic of trees. PNAS Nexus, 4, 2, pgaf003. https://doi.org/10.1093/pnasnexus/pgaf003